Der Barthel'sche Transformationszirkel

Abb. 1: Der stolze Erfinder mit seinem Transformationszirkel in einer Publikation von 1931 [1].

Dieser Artikel ist einer geometrischen Idee von Ernst Barthel aus den 1920er Jahren gewidmet. Die Idee beruht auf der Überlagerung zweier Kreisbewegungen, aber nicht als Abrollfigur, sondern als konzentrische Verkopplung. Der Umlaufarm des tragenden, inneren Kreis führt das Drehzentrum das äußeren Kreises mit sich. Dies ist etwas qualitativ anderes als die sonst bekannten Kreisabrollungen bei Epi- und Hypotrochoide (auch genannt Zykloide).

Durch die konzentrische Verkopplung entsteht durch Variation der Radien R₁ und R₂ und Umlaufdauern w₁ und w₂ eine erstaunliche Formenvielfalt. Barthel entwickelte zur Veranschaulichung seiner Idee in den 1930er Jahren ein mechanisches Zeichengerät (Abb. 1), den sog. "Transformationszirkel", den er damals auch patentieren ließ. In Abb. 2 ist er gezeigt, zusammen mit einigen Kurven, die mit dem Transformationszirkel gezeichnet wurden.

Abb. 2: Eine Fotographie das mechanischen Transformationszirkels aus [2] S. 169.

Entscheidend an der Barthel`schen Kreisverkopplung ist die vierfältige Interpretations-möglichkeit eines gegeben Parametersatzes R₁, R₂ und w₁, w₂. Einerseits können die Kreisumläufe entweder gleich- oder gegensinnig sein, und andererseits kann jeder Kreis entweder als Träger oder Getragener fungieren. Die jeweils entstehenden Figuren unterscheiden sich erheblich (s.u. und Abb. 3). Was in den 1930er Jahren jedoch noch mechanischen Aufwands bedurfte, lässt sich heute bequem computergraphisch veranschaulichen.

Der Transformationszirkel-Simulator

Auf dieser Seite oben befindet sich eine interaktive Simulation des Transformationszirkels, die ich einmal mit Unity3D und einmal zur Betrachtbarkeit auf Handys etwas einfacher in html5 umgesetzt habe. Die zentralen Bedienelemente sind die Slider rechts für die Umlaufdauern w₁ und w₂ sowie für das Radiusverhältnis R₁/R₂. Rechts lassen sich über die Knöpfe direkt die Kreisfunktionen austauschen ("Funktionskomplement"), d.h. der innere mit dem äußeren Kreis vertauschen, sowie auch der Richtungssinn der beiden Umläufe ("Richtungskomplement"). Mit dem Häkchen "Zeige Konstruktion" und dem Knopf "Neu zeichnen" kann sich außerdem die Konstruktion der Kurven animieren lassen. Daneben existieren noch einige Zusatzoption, wie z.B. die akustische Umsetzung der y-Komponente der Schwingungen als wav-Datei, oder die Anzeige der beteiligten analytischen und algebraischen Frequenzen in der Unity-Version.
... Analytische UND algebraische Frequenz!? Ja, sie haben richtig gelesen, und es gibt tatsächlich einen Unterschied zwischen beiden, der vor allem für die Möglichkeiten der physikalischen Interpretation des Transformationszirkels bedeutsam wird. Anschaulich gesehen benötigt man die Unterscheidung nicht, denn die Umlaufdauern w_i sind einfach schon eine Frequenz im Sinne einer Anzahl von Umläufen pro Zeiteinheit. Doch wenn man dem Computer beibringen will, wie er die w_i zu deuten hat, dann genügt diese Anschauung nicht. Wir müssen die Anschauung auf ein Koordinatensystem bringen, das sowohl unsere Anschauung repräsentiert als auch programmierbar ist. Praktisch nützlich ist dafür ein kartesisches 2D-Koordinatensystem.

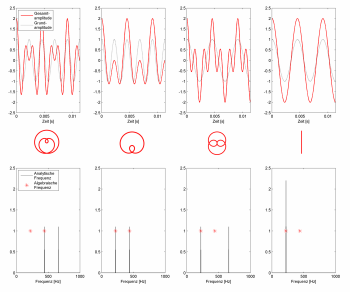
Abb. 3: Alle vier Komplementärmöglichkeiten für gleiche Radien und ein Umlaufverhältnis von 1:2. Dargestellt sind die Schwingungen in y-Richtung für den inneren Kreis sowie das Gesamtsystem. Analytisch betrachtet haben alle vier Fälle unterschiedliche Frequenzzusammensetzung, während algebraisch bzw. geometrisch jeweils genau die gleichen Frequenzen vorliegen. Eine akustische Übertragung lässt sich hier abspielen: 1: , 2: , 3: , 4: .

Die Formel für die graphische Repräsentation der konzentrischen Kreisverkopplung lautet dann:

x(t) = R₁sin[w₁t] + R₂sin[(w₁ + w₂)t]
y(t) = R₁cos[w₁t] + R₂cos[(w₁ + w₂)t]

Mit genau dieser Formel werden die Kurven in der Simulation oben gezeichnet, wobei t der Laufparameter ist. Eine 1D-Darstellung entlang des Laufparameters ist in Abb. 3 dargestellt. Darin ist unten auch eine (fourier-)analytische Frequenzzerlegung gezeigt, zusammen mit den Frequenzen der einzelnen Umläufe. Die analytischen Frequenzen sind nun NICHT gleich den "algebraischen" Einzelkreisfrequenzen! Erkenntnismäßig handelt es sich dabei durchaus um keine Kleinigkeit.

Physikalische Interpretationen des Transformationszirkels

Analytische Frequenzen oder das Spektrum eines Phänomens werden häufig zur technischen Beschreibung verwendet. Oft wird das Spektrum auch als vollständiges Charakteristikum aufgefasst, z.B. für Farb- oder Höreindrücke, oder für chemische Elemente. Und das Spektrum erlaubt auch die technische Reproduktion von Farb- und Höreindrücken. Man kann also verstehen, warum es in der Physik beliebt ist, das Spektrum auch als physikalisches Grundphänomen oder schlicht als "real" zu bezeichnen. Doch was heißt "real" hier? Streng genommen nur, dass der Kreis von der Vermessung eines Phänomens über seine technische Reproduktion bis hin zur Wahrnehmung der Reproduktion geschlossen erscheint. Üblicherweise will man gar nicht mehr - denn wie alle Flachkantianer wissen, kann man auch nicht mehr erkennen als Schein.
Fakt bleibt, dass hier ein Beispiel vorliegt, bei der zwei unterschiedliche Frequenzpaare das gleiche Phänomen beschreiben. Beide Beschreibungen sind äquivalent, aber mit qualitativ unterschiedlicher Struktur: Die analytischen Frequenzen betonen dabei die technische Reproduzierbarkeit, die algebraischen die Verwandtschaft einer Phänomengruppe (z.B. der Zusammenhang der Kurvenkomplemente). Welche Beschreibung einem besser gefällt, unterliegt der individuellen Deutungsfreiheit. Ob ich ein Frequenzgemisch F als F = f₁ + f₂ oder als F = f₃ + (f₄+ ... + f_n) kann einem niemand vorschreiben.
Genauso wenig kann man vorschreiben, ob man mit einer exakten Frequenz eine gleichmäßige, andauernde Schwingung meint, oder den zeitlichen Abstandes zwischen zwei Nulldurchgängen. Analytisch und verbreitet ist die erste Frequenz, weil sie als Ergebnis einer mathematischen Analyse per sog. Fouriertransformation bestimmt werden kann. Anschaulich ist dagegen die manuelle Ausmessung von Nulldurchgängen. Die stillschweigende Konventionen zugunsten der analytischen Frequenz hat zum Beispiel den Protagonisten der Wetterstrahlung einige Schwierigkeiten bereitet. In der Physik liebt man Konvention mehr als tiefe Naturerkenntnis, und man ahnt die Ursache der leisen Unruhe angesichts der Deutungsfreiheit, die bei jedem Experiment oder Naturphänomen unzweifelhaft besteht.
Ernst Barthel hat seinerzeit einen kühnen Schritt gewagt, das Thema der naturwissenschaftlichen Deutungsfreiheit systematisch auszuloten. Er stand damit in der Tradition von u.a. Henri Poincaré, der das Prinzip des physikalischen Konventionalismus prägte. Ernst Barthel hat sich im Gegensatz zu Poincaré nicht gescheut, altehrwürdige Überzeugungen scharf zu kritisieren und im Zweifelsfall durch neue, seiner Auffassung nach bessere zu ersetzen.
Mit aus diesem Grunde hat er seinen Transformationszirkel und dessen Komplementaritätsbeziehungen als Analogon zur Goethe`schen Farbtheorie [3] verstanden. In einem unscheinbaren Artikel von 1938 [4] wagt er die Behauptung, dass die Newton'schen Farbtheorie Unsinn und die Goethe'sche "richtig" sei! Er behauptet, Farben seien schwingungsmäßige Zweikreisverkopplungen - genau wie sie der Transformationszirkel zeichnet. Als Beweis für die Goethe'sche Farbtheorie und seine Spezifizierung legt er die Fähigkeit der Zweikreisverkopplung zur Komplementbildung vor. Die algebraische Überlagerung zweier Kurvenkomplemente liefert einen einfachen Kreisumlauf - d.h. weißes Licht Goethe`scher Lesart, aus z.B. orange und blau. Ich will nicht weiter ausführen, wie die Welt der Physik damals auf diese verstörend einfache Idee reagiert hat...wer glaubt, dass wir heute gegenüber damals noch Nachholbedarf haben könnten, der oder die sei auf die Referenzen [3-5] verwiesen.

Ein 2D-transzendenter Ausblick

Hübsch sind sie definitiv, die Kurven des Transformationszirkels. Und wie so oft geht vom Hübschen ein eigentümlicher Sog aus, dem sich niemand ohne Not entziehen will. Wer unter R₁ 314 eingibt, kann einen Ausflug in einen verstörenden Ausläufer ähnlicher Prägung wagen. Dieser 'magic string' eröffnet den Weg der Kurven in die dritte Dimension. Die Beziehung der 3D-Geschwister zum Barthel'schen Zirkel scheint mir noch einige Überraschungen zu bergen, angesichts der mutmaßlichen oder vermeintlichen Herkunft [6] der Geschwister. Ich will ich mich hier jedoch vorerst eines Kommentars enthalten.
Ganz im Gegensatz zu Ihnen lieben Leserinnen und Lesern, die Sie unten gerne Ihre Meinung oder Anregung hinterlassen dürfen. Gern können Sie auch ihre persönlichen Lieblingsparameter beifügen.
Denn die DEUTUNGSFREIHEIT ist die Kraft der Zukunft!

Literatur

1. Rollkurven können mechanisch aufgezeichnet werden. In: Technische Blätter der Deutschen Bergwerkszeitschrift, S.314, 26. April 1931
2. Ernst Barthel: Einführung in die Polargeometrie. Verlag Robert Noske, Leipzig, 1932
3. Ernst Barthel: Goethes Relativitätstheorie der Farbe. Nebst einer musikästhetischen Parallele. Verlag Friedrich Cohen, Bonn, 1923
4. Ernst Barthel: Komplementaristische Wellenmechanik. Eine Rechtfertigung der Goethe'schen Farbenlehre. In: Jahrbuch der Elsaß-Lothringischen Wissenschaftlichen Gesellschaft zu Straßburg, S. 240-251, 1938.
5. Ernst Barthel: Mensch und Erde im Kosmos. Verlag für Volkskunst und Volksbildung, Richard Keutel, Lahr (Baden) 1939
6. Stefan Denaerde & Wendelle C. Stevens: UFO contact from planet IARGA. Selbstverlag Wendelle C. Stevens, 1982

Kommentare

Name:

Kommentar:

(Bitte Code abtippen.)

Abgegebene Kommentare:

ElliotUnuse schrieb am 06.12.2020 um 16:03:10 Uhr:

rash home remedies <a href=https://www.bizcommunity.com/Profile/Phentermineonlinekaufenohne>https://www.bizcommunity.com/Profile/Phentermineonlinekaufenohne</a> kindred health care

KelSalfut schrieb am 07.10.2019 um 19:56:05 Uhr:

Cialis Apotheke Online Viagra Sans Ordonnance Belgique Phenergan Without Prescription Fast <a href=http://cialviag.com>cheap cialis</a> Levitra Selbst Gemacht Acheter Cialis Site Serieux Comprar Cialis Y Priligy

Weltall Erde Mensch schrieb am 21.12.2014 um 22:44:22 Uhr:

Als Barthelfreund bedanke ich mich für den Artikel und das Veranschaulichungswerkzeug.